Healthcare Pricing and Competition

Author

Ian McCarthy | Emory University

Table of contents

  1. Competition in Theory
  2. Competition in Practice

Competition in Theory

Fixed Prices

  • Demand: \(q_{j}=s_{j}(z_{j}) \times D(\bar{p})\)
  • Costs: \(c_{j}=c(q_{j},z_{j}) + F\)
  • Profits: \(\pi_{j} = \bar{p}q_{j} - c_{j}\)

Hospitals choose quality such that: \[\frac{\partial \pi_{j}}{\partial z_{j}} = \left(\bar{p} - \frac{\partial c_{j}}{\partial q_{j}} \right)\left(\frac{\partial s_{j}}{\partial z_{j}}D + s_{j}\frac{\partial D}{\partial z_{j}} \right) - \frac{\partial c_{j}}{\partial z_{j}}=0\]

Fixed Prices

  • Increase in competition will tend to increase quality
  • Negative welfare effects if \(\frac{\partial D}{\partial z_{j}}\) is sufficiently small and fixed costs are large

Fixed Prices

Alternative expression for quality: \[z_{j} = \left(\bar{p} - c_{q} \right) \left(\eta_{s} + \eta_{D} \right) \frac{D s_{j}}{c_{z}}\]

  • Quality increasing in \(\bar{p}\)
  • Quality increasing in share and demand elasticities
  • Quality increase in overall market share and market demand
  • Quality decreasing in marginal cost

Market Prices

Profit given by \(\pi = q(p,z) \times (p-c-d\times z) - F,\) which yields

\[\begin{align*} p &= \frac{\epsilon_{p}}{\epsilon_{p}-1} (c+dz) \\ z &= \frac{\epsilon_{z}}{\epsilon_{z}+1} \frac{p-c}{d} \end{align*}\]

Market Prices

Rewrite in terms of elasticities:

\[\begin{align*} \epsilon_{p} &= \frac{p}{p-c-dz} \\ \epsilon_{z} &= \frac{dz}{p - c - dz} \end{align*}\]

Taking the ratio and solving for \(z\) yields, \[z = \frac{p}{d}\times \frac{\epsilon_{z}}{\epsilon_{p}}.\]

Market Prices

\[z = \frac{p}{d}\times \frac{\epsilon_{z}}{\epsilon_{p}}\]

Dorfman-Steiner condition:

  • Quality increases if the quality elasticity increases or if price increases
  • Quality increases if the price elasticity decreases or the marginal cost of quality decreases

Prediction for competition: Hospitals will compete on whatever matters most to patients.

Bargaining

Basic Bargaining Model

Gowrisankaran, Nevo, and Town extend the Nash bargaining framework to consider a hospital-insurer negotiation. They propose a two-stage bargaining process:

  1. Hospitals and insurers negotiate over the terms of their agreement (network inclusion and prices)
  2. Individuals receive “health draws” which dictate their healthcare needs

Bargaining occurs over a base price, not specific to each procedure

Basic Bargaining Model

  • Total expected cost to the insurer, \(TC_{m}(N_{m},\vec{p}_{m})\)
  • Willingness to pay to have access to hospital, \(W_{m}(N_{m},\vec{p}_{m})\)
  • Total payoff for the MCO is \[V_{m}(N_{m},\vec{p}_{m}) = \tau W_{m}(N_{m},\vec{p}_{m}) - TC_{m}(N_{m},\vec{p}_{m}),\] where \(\tau\) is the relative weight placed on employee/patient welfare
  • Net value that MCO \(m\) receives from including hospital \(j\) in its network is then \(V_{m}(N_{m},\vec{p}_{m})-V_{m}(N_{m,-j},\vec{p}_{m})\).

Basic Bargaining Model

In the case of a single hospital system, and denoting hospital \(j\)’s marginal cost for services provided to patients in MCO \(m\) is given by \(mc_{mj}\), the overall profit for hospital \(j\) for a given set of MCO contracts (denoted \(M_{s}\)), is \[\pi_{j}\left(M_{s},\{\vec{p}_{m}\}_{m\in M_{s}} \right)=\sum_{m\in M_{s}} q_{mj}(N_{m},\vec{p}_{m}) \left[p_{mj} - mc_{mj} \right].\]

Basic Bargaining Model

The authors then derive the Nash bargaining solution as the choice of prices maximizing the exponentiated product of the net value from agreement:

\[\begin{align*} NB^{m,j} \left(p_{mj} | \vec{p}_{m,-j}\right) &= \left(q_{mj}(N_{m},\vec{p}_{m}) \left[p_{mj} - mc_{mj} \right]\right)^{b_{j(m)}} \\ & \times \left(V_{m}(N_{m},\vec{p}_{m})-V_{m}(N_{m,-j},\vec{p}_{m})\right)^{b_{m(j)}}, \end{align*}\]

where \(b_{j(m)}\) is the bargaining weight of hospital \(j\) when facing MCO \(m\), \(b_{m(j)}\) is the bargaining weight of MCO \(m\) when facing hospital \(j\), and \(\vec{p}_{m,-j}\) is the vector of prices for MCO \(m\) and hospitals other than \(j\). We can normalize bargaining weight such that \(b_{j(m)} + b_{m(j)} = 1\).

Basic Bargaining Model

Taking the natural log, the resulting first order condition yields:

\[\begin{align*} \frac{\partial \ln (NB^{m,s})}{\partial p_{mj}} =& b_{s(m)} \frac{q_{mj} + \frac{\partial q_{mj}}{\partial p_{mj}} \left[p_{mj}-mc_{mj}\right]}{q_{mj}\left[p_{mj}-mc_{mj}\right]} \\ & + b_{m(j)} \frac{\frac{\partial V_{m}}{\partial p_{mj}}}{V_{m}(N_{m},\vec{p}_{m})-V_{m}(N_{m,-j},\vec{p}_{m})} = 0 \end{align*}\]

Basic Bargaining Model

Simplifying and rewriting, we get: \[p_{mj} - mc_{mj} = -q_{mj} \left(\frac{\partial q_{mj}}{\partial p_{mj}} + q_{mj} \times \frac{b_{m(j)}}{b_{j(m)}} \times \frac{\frac{\partial V_{m}}{\partial p_{mj}}}{\triangle V_{m}} \right)^{-1}\]

  • \(\triangle V_{m}\) is positive by construction
  • Can show that \(\frac{\partial V_{m}}{\partial p_{mj}}<0\) under most conditions

Bargaining tends to increase the “effective” price sensitivity and reduce hospital margins relative to standard pricing conditions (but not always)

Basic Bargaining Model

  • Price response to other changes depends largely on \(\frac{\partial V_{m}}{\partial p_{mj}}\)
  • Can be expressed as: \[-q_{mj}-\alpha \sum_{i}\sum_{d}\gamma_{id}c_{id}(1-c_{id}) \left(\sum_{k\in N_{m}} p_{mk}s_{ikd} - p_{mj}\right),\] where \(\gamma_{id}\) includes several terms including disease weights and probability of disease.

Basic Bargaining Model

\[-q_{mj}-\alpha \sum_{i}\sum_{d}\gamma_{id}c_{id}(1-c_{id}) \left(\sum_{k\in N_{m}} p_{mk}s_{ikd} - p_{mj}\right),\]

  • \(c_{id}\) denotes the coinsurance rate
  • final term is the difference between hospital \(j\)’s price and the weighted average price of all other hospitals (weighted by their market share)
  • \(c_{id}\times (1-c_{id})\) shows role of coinsurance in steering patients to different hospitals

Competition in Practice

Key Issues

  1. Measuring competitiveness
  2. Reduced form - mergers, closures, structure-conduct-performance
  3. Structural estimation with bargaining models

Measuring competitiveness

  • Common measure is Herfindahl-Hirschman Index (HHI), \(\sum_{i=1}^{N} s_{i}^{2}\).
    • 2,500 is considered highly concentrated
    • 1,800 is considered unconcentrated
  • “Willingness to pay” is more recent measure (theoretically supported)
  • Both require a measure of the geographic market

Defining the market

Lots of subjectivity…

  • Radius around a hospital?
  • Concentric circles to define “catchment” areas?
  • Patient/physician referrals?
  • At what product-level do hospitals compete?

Hospital concentration over time

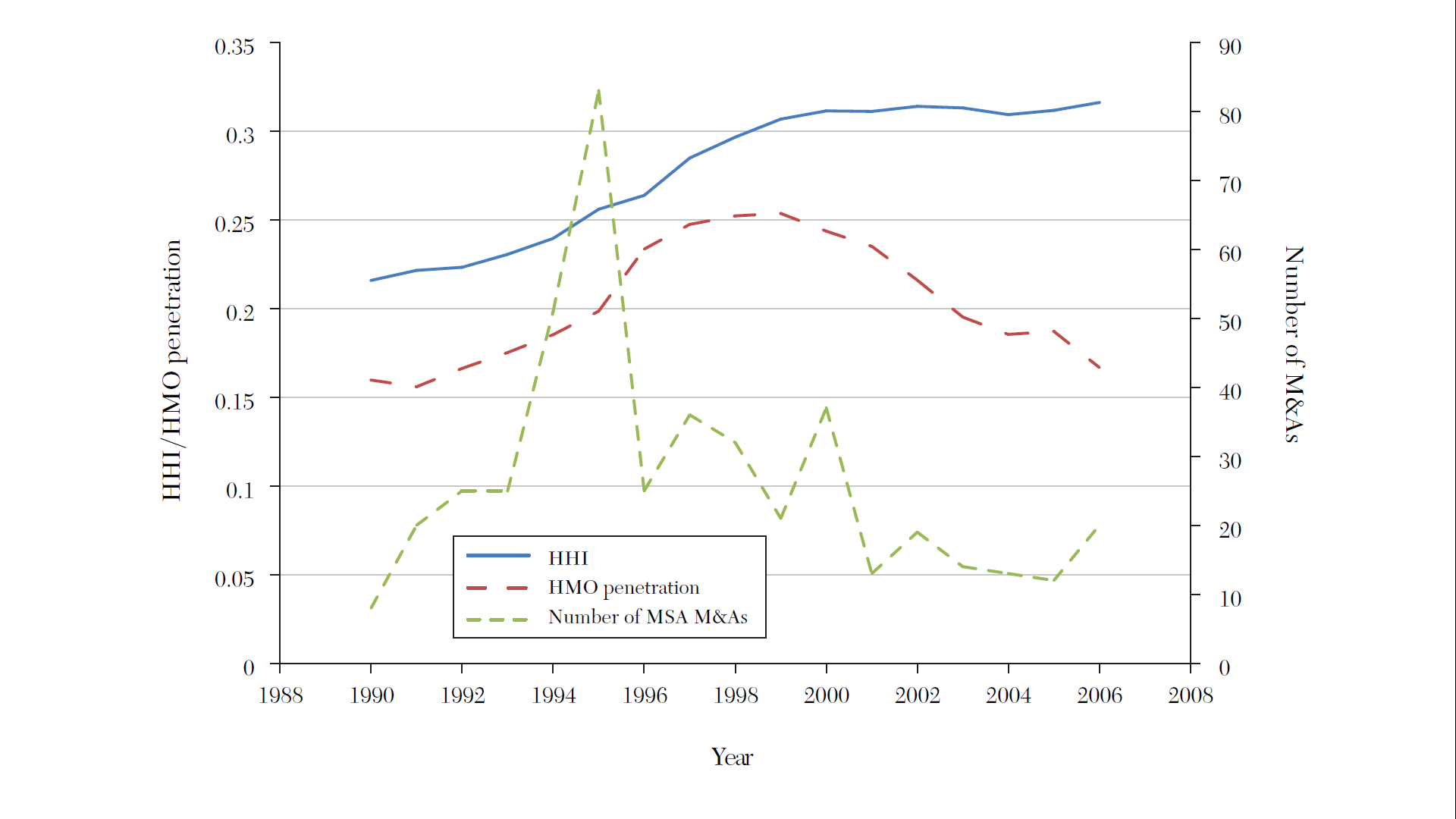
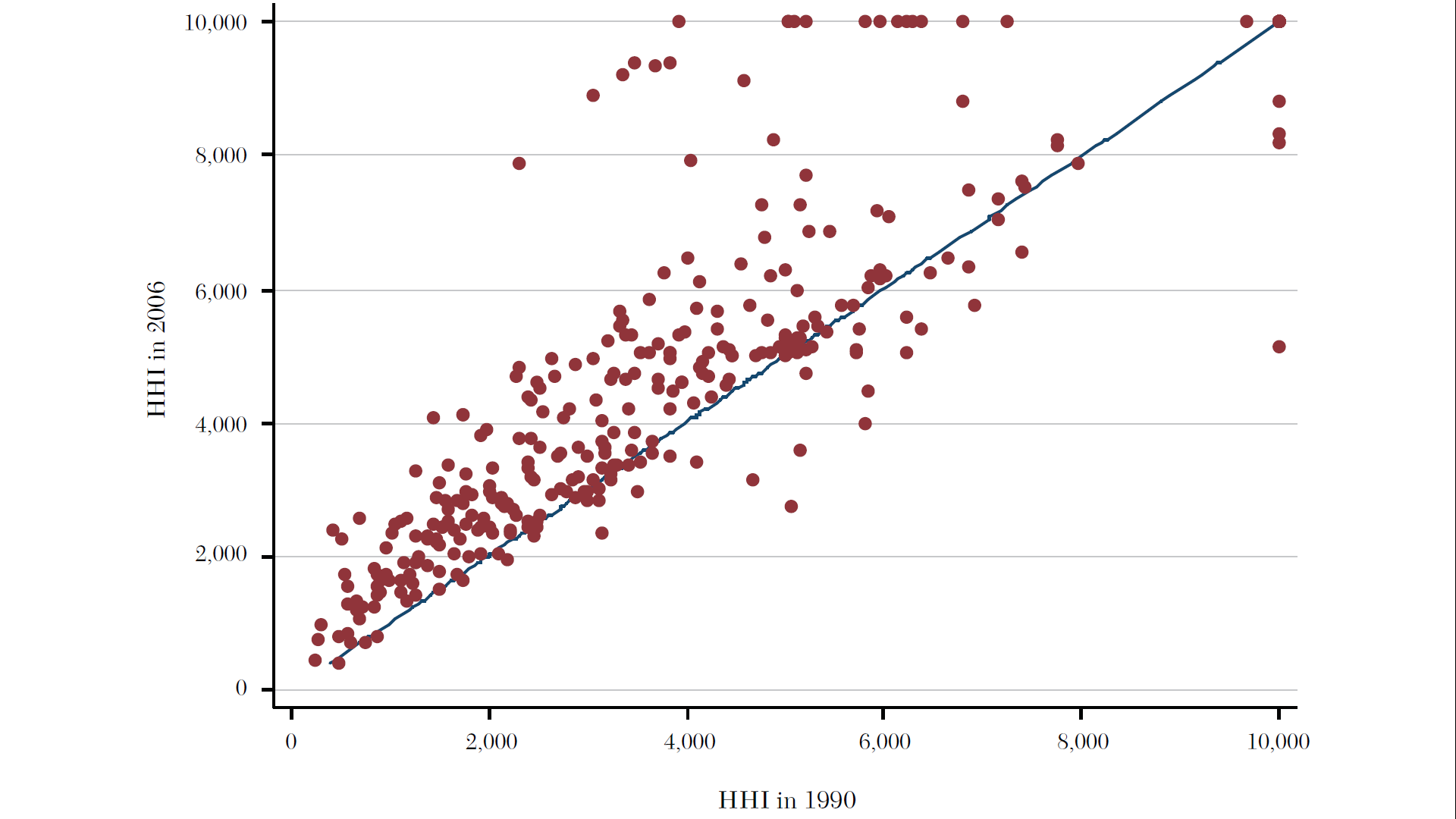
Source: Gaynor, Ho, and Town (2015). The Industrial Organization of Health Care Markets. Journal of Economic Literature.

Hospital concentration over time

Why?

Historical perception of hospital competition as “wasteful” and assumption that more capacity means more (unnecessary) care:

  • Limit public spending by limiting competition
  • Prevalence of certificate of need (CON) laws

Effects of reduced competition

  1. Higher prices
  2. Lower quality, 2020 NEJM Paper
  3. Maybe lower costs (but not passed on to lower prices)

Effects for both “in-market” and “out-of-market” mergers

Measuring Competition

Importance of the market

Every analysis of competition requires some definition of the market. This is complicated in healthcare for several reasons:

  1. Hospital markets more local than insurance markets
  2. Hospitals are multi-product firms
  3. Geographic market may differ by procedure
  4. Insurance networks limit choice within a geographic market

Given a market

Once we have a measure of the market, we’d like to have a quick and easy way to assess competitiveness:

  1. HHI
  2. WTP

HHI

  • Basic Cournot framework: \[\pi_{i} = P(q) q_{i} - C_{i}(q_{i})\]
  • First order condition: \[P'(q) q_{i} + P(q) - C_{i}'(q) = 0\]

HHI

  • Rewriting yields: \[\frac{P(q) - C_{i}'(q_{i})}{P(q)} = \frac{q_{i}}{q} \times \frac{-P'(q)q}{P(q)}=\frac{\alpha_{i}}{\eta}\]
  • Constant marginal costs: \[\frac{p - c_{i}}{p} = \frac{\alpha_{i}}{\eta}\]

HHI

  • In equilibrium, \[\sum_{i}\pi_{i} = \sum_{i}(p - c_{i}) q_{i} = \sum_{i}(p-c_{i})\alpha_{i} q\]
  • Two equivalent expressions
    • \(\sum_{i} \pi_{i} = \left(p - \sum_{i} \alpha_{i} c_{i} \right)q\) and
    • \(\sum_{i} \pi_{i} = \frac{pq}{\eta} \sum_{i} \alpha_{i}^{2}\) after substituting \(p - c_{i} = \alpha_{i} \frac{p}{\eta}\).

HHI

  • Equating these two expressions yields:\[\frac{p - \sum_{i} \alpha_{i} c_{i}}{q} = \frac{\sum_{i} \alpha_{i}^{2}}{\eta} = \frac{HHI}{\eta}\]
  • Takeaway: In linear Cournot model with constant marginal costs and homogeneous products, the markup (a common measure of market power) is proportional to the HHI.

WTP

  • Alternative measure from Capps et al. (2003)
  • Not healthcare specific…option demand market where indermediary sells a “network” of products to consumers, and consumers are uncertain about final products they will need
  • Key: consumers agree to ex ante restrict their choice set before they know what services are needed
  • Derivation works backward…

WTP

Step 1. Derive ex post utility.

\[\begin{align*} U_{ij} &= \alpha R_{j} + H_{j}'\Gamma X_{i} + \tau_{1} T_{ij} + \tau_{2} T_{ij} X_{i} + \tau_{3} T_{ij} R_{j} - \gamma(Y_{i},Z_{i}) P_{j}(Z_{i}) + \varepsilon_{ij} \\ &= U(H_{j},X_{i},\lambda_{i}) - \gamma(X_{i})P_{j}(Z_{i}) + \varepsilon_{ij}, \end{align*}\]

which yields choice probabilities, \[s_{ij} = s_{j}(G,X_{i},\lambda_{i}) = \frac{\text{exp}(U(H_{j},X_{i},\lambda_{i}))}{\sum_{g\in G}\text{exp}(U(H_{g},X_{i},\lambda_{i}))}.\]

WTP

Step 2. Derive utility from access to network, \(G\), with \(U(H_{g},X_{i},\lambda_{i})\) taken as given.

The patient’s expected maximum utility across all hospitals is, \[V(G,X_{i},\lambda_{i}) = \text{E} \left[\max_{g\in G} U(H_{g},X_{i},\lambda_{i}) + \varepsilon_{g} \right] = \text{ln} \left[\sum_{g\in G} \text{exp} (U(H_{g},X_{i},\lambda_{i})) \right].\]

WTP

Contribution of hospital \(j\) is then:

\[\begin{align*} \triangle V_{j}(G,X_{i},\lambda_{i}) &= V(G,X_{i},\lambda_{i}) - V(G_{-j},X_{i},\lambda_{i}) \\ &= \text{ln} \left[ \left(\sum_{k\in G_{-j}} \frac{ \text{exp} (U(H_{k},X_{i},\lambda_{i})) }{\sum_{g\in G} \text{exp} (U(H_{g},X_{i},\lambda_{i})) }\right)^{-1} \right] \\ &= \text{ln} \left[ \left(\sum_{k\in G_{-j}} s_{k}(G,X_{i},\lambda_{i})\right)^{-1} \right] \\ &= \text{ln} \left[ \left( 1- s_{j}(G,X_{i},\lambda_{i})\right)^{-1} \right]. \end{align*}\]

WTP

Translate into dollar values by weighting by the marginal utility of price \[\triangle \tilde{W}_{j} = \frac{\triangle V_{j}}{\gamma (X_{i})}.\]

WTP

Step 3. Estimate ex ante WTP to include hospital \(j\) in patient’s network. (i.e., integrate over all possible health conditions)

\[W_{ij}(G,Y_{i},\lambda_{i}) = \int_{Z} \frac{\delta V_{j}(G,X_{i},\lambda_{i})}{\gamma (X_{i})} f(Z_{i}|Y_{i},\lambda_{i}) dZ_{i}.\]

Further integrating over all patients, \((Y_{i},\lambda_{i})\), yields \[WTP_{j} = N \int_{\lambda} \int_{Z} \int_{Y} \frac{1}{\gamma (X_{i})} \text{ln}\left[\frac{1}{1-s_{j}(G,X_{i},\lambda_{i})} \right]f(Y_{i},Z_{i},\lambda_{i})dY_{i} dZ_{i} d\lambda_{i}.\]

WTP in Practice

Simplify by calculating WTP for each “micro-market” (e.g., health condition) and taking sum:

\[WTP_{j} = - \sum_{m} N_{m} \text{ln}(1 - s_{mj})\]